Prediction

Suggested Answers

library(tidyverse)

Warning: package 'ggplot2' was built under R version 4.2.2

Warning: package 'tidyr' was built under R version 4.2.2

Warning: package 'readr' was built under R version 4.2.2

Warning: package 'purrr' was built under R version 4.2.2

library(tidymodels)

Warning: package 'broom' was built under R version 4.2.2

Warning: package 'dials' was built under R version 4.2.2

Warning: package 'parsnip' was built under R version 4.2.2

Warning: package 'recipes' was built under R version 4.2.2

library(ggridges)

Warning: package 'ggridges' was built under R version 4.2.2

library(patchwork)
library(palmerpenguins)

By the end of today, you will…

• Practice calculating AIC
• Understand the ideas behind testing vs training data sets
• (continued) fit a logistic regression model in R
• Evaluate your model based on predictions

We will again be working with the email data set. Please re-familiarize yourself with these data below:

email <- read_csv("data/email.csv") |>
  mutate(spam = factor(spam),
         image = factor(image),
         winner = factor(winner))

Rows: 3890 Columns: 21
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr   (2): winner, number
dbl  (18): spam, to_multiple, from, cc, sent_email, image, attach, dollar, i...
dttm  (1): time

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

#|label: glimpse

glimpse(email)

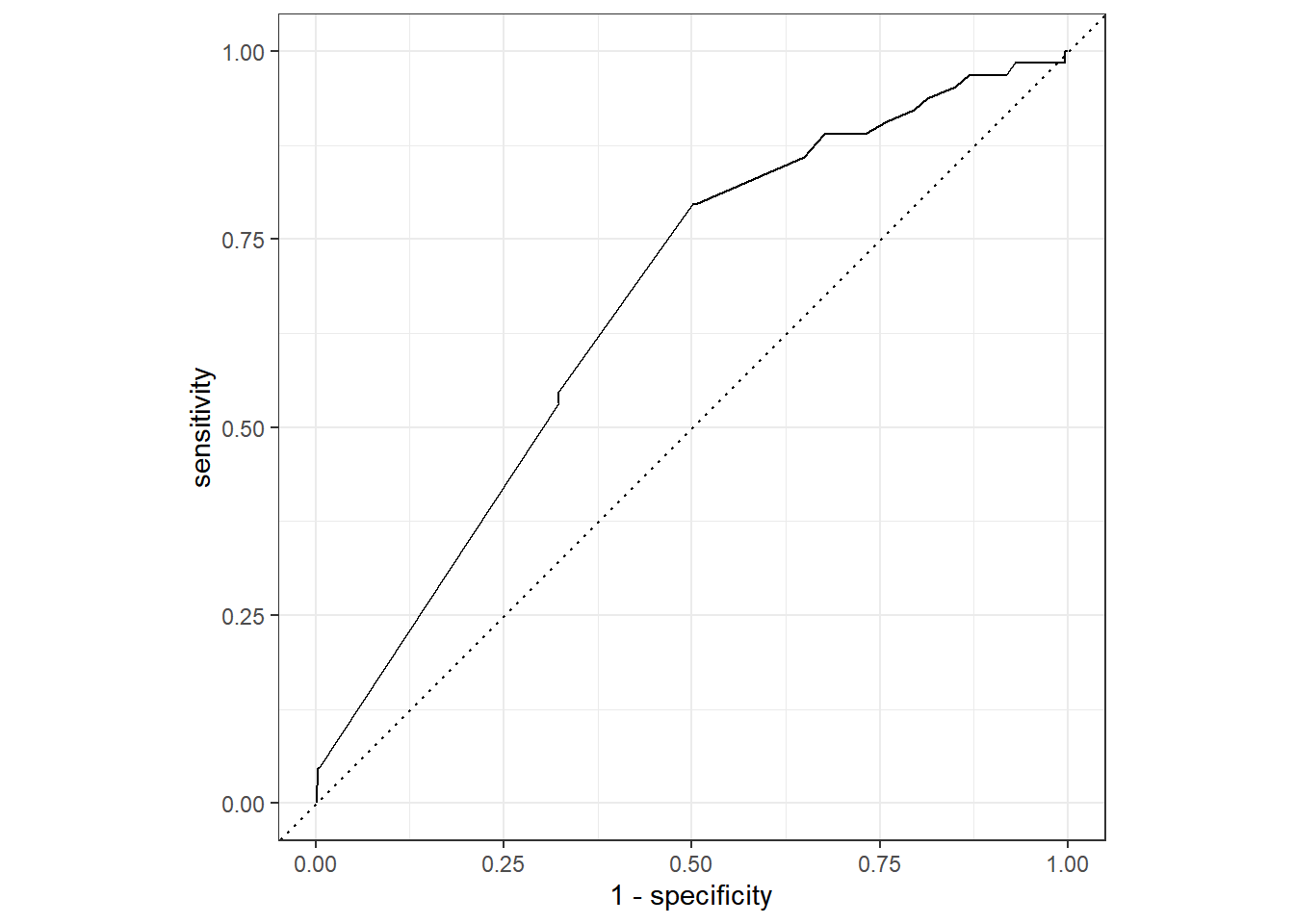
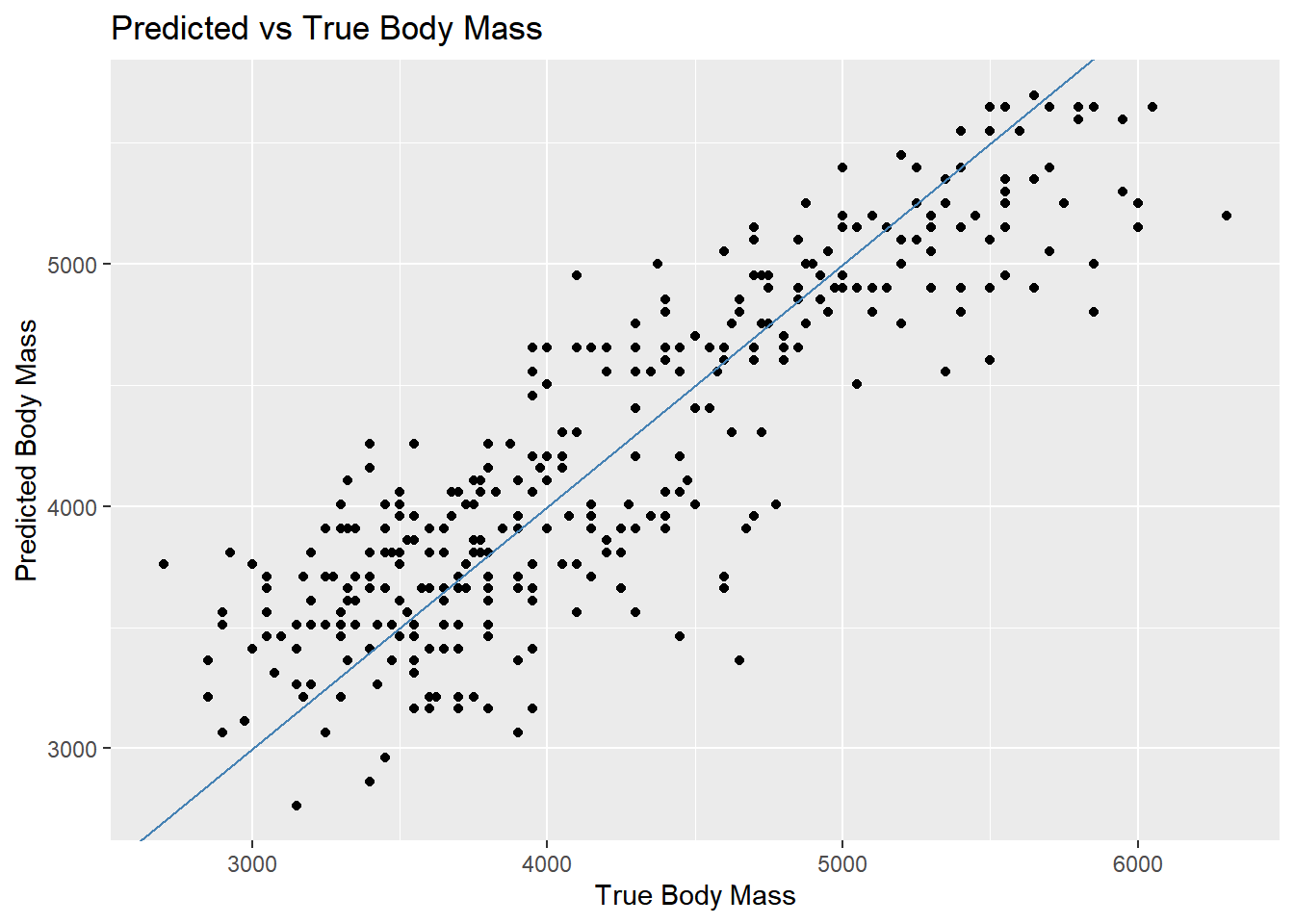
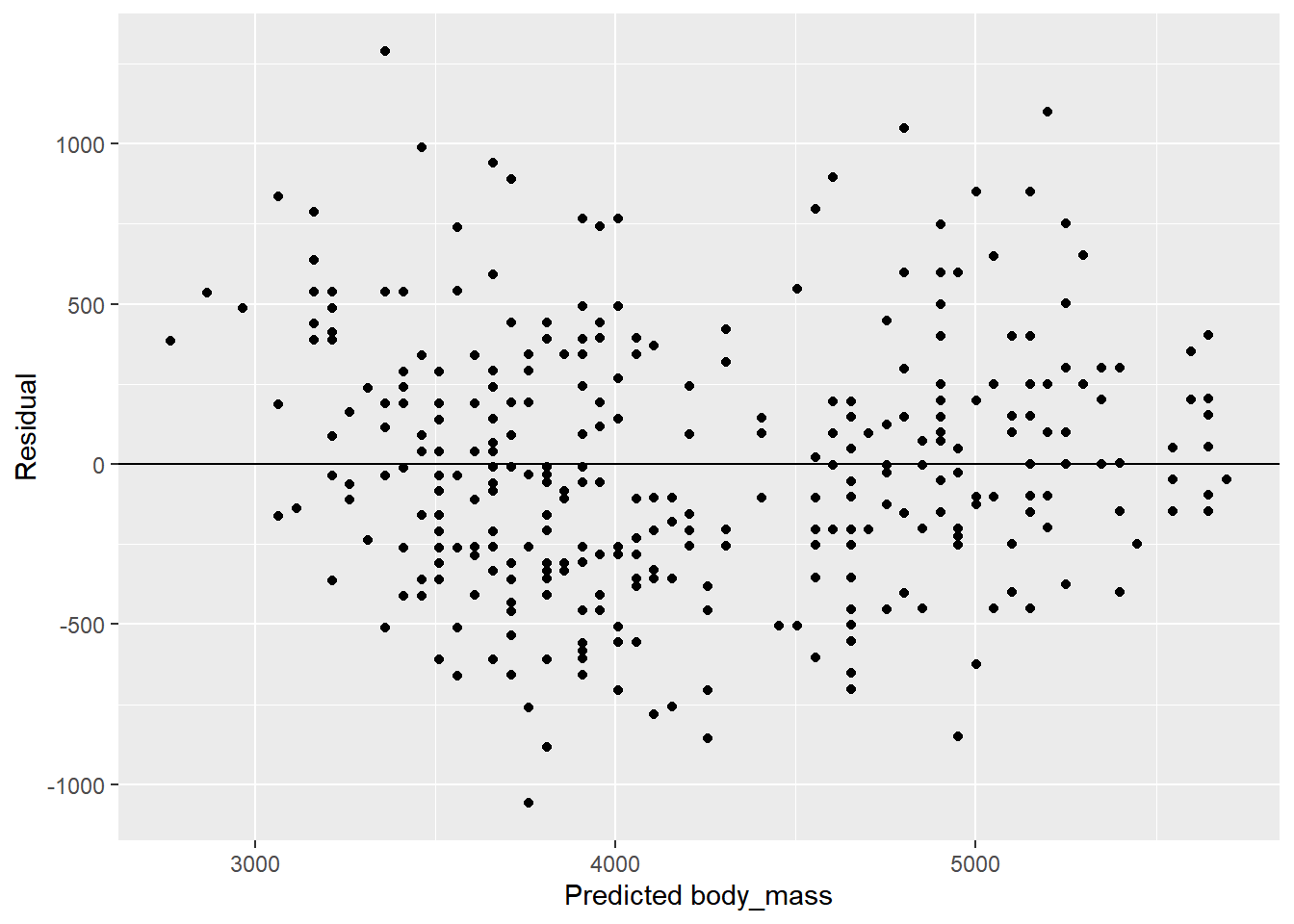
Rows: 3,890
Columns: 21
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ from         <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 2, 1, 0, 2, 0, …
$ sent_email   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, …
$ time         <dttm> 2012-01-01 06:16:41, 2012-01-01 07:03:59, 2012-01-01 16:…
$ image        <fct> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ attach       <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 5, 0, 0, …
$ winner       <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…
$ inherit      <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ num_char     <dbl> 11.370, 10.504, 7.773, 13.256, 1.231, 1.091, 4.837, 7.421…
$ line_breaks  <dbl> 202, 202, 192, 255, 29, 25, 193, 237, 69, 68, 25, 79, 191…
$ format       <dbl> 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, …
$ re_subj      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, …
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ urgent_subj  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 10, 4, 10, 20, 0…
$ number       <chr> "big", "small", "small", "small", "none", "none", "big", …

Much like in the multiple linear regression case, we can have multiple predictors to model our categorical response. See example below:

logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ exclaim_mess + winner, data = email) |>
  tidy()

# A tibble: 3 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    -1.95     0.0648    -30.1  7.33e-199
2 exclaim_mess   -0.173    0.0239     -7.26 3.89e- 13
3 winneryes       1.88     0.307       6.13 8.84e- 10

Based on this output, is it more or less likely an email is spam if the email contains the phrase “winner”, after holding the number of exclamation points constant?

More likely. 1.88 is positive

What is the predicted probability of an email being spam if there is only 1 exclamation point, and the email contains the phrase winner?

How much does the probability increase/decrease if the email does not contain the phrase “winner”?

email_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ exclaim_mess + winner, data = email, family = "binomial") 


new_email <- tibble(exclaim_mess = 1, winner = "yes" )

predict(email_fit$fit, new_email, type = "response") # probability

        1 
0.4405064 

(5-min) The person responsible for this model claims that this is the best model to classify emails as spam. Below, calculate the AIC for their model. Then, create a model that is “better” based on AIC evidence.

glance(email_fit)$AIC

[1] 2293.629

class_model <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ line_breaks + dollar + winner, data = email , family = "binomial")

glance(class_model)$AIC

[1] 2220.657

Prediction

For the next portion, we are going to compare predictive performance between two models.

The variables we’ll use for the first model will be:

• spam: 1 if the email is spam, 0 otherwise
• exclaim_mess: The number of exclamation points in the email message
• winner: Has the word “winner” in the email or not

The variables we’ll use for the second model will be:

• spam: 1 if the email is spam, 0 otherwise
• exclaim_mess: The number of exclamation points in the email message
• image: Had an image attached to the email

Testing vs Training

Let’s build a testing and training data set using the following code.

– Go through line by line and comment what the code is doing…

Once complete, take a glimpse at each new data set.

set.seed(0610) 

email_split <- initial_split(email, prop = 0.80) 

train_data <- training(email_split)
test_data <- testing(email_split)

glimpse(test_data)

Rows: 778
Columns: 21
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, …
$ from         <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <dbl> 0, 2, 0, 0, 2, 0, 0, 0, 0, 3, 0, 1, 0, 0, 0, 1, 0, 0, 2, …
$ sent_email   <dbl> 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, …
$ time         <dttm> 2012-01-01 10:00:01, 2012-01-01 23:32:53, 2012-01-02 01:…
$ image        <fct> 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ attach       <dbl> 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 0, 2, 0, 9, 0, 0, 0, 2, 0, 0, 6, 0, 0, 0, 0, 0, 0, 0, 0, …
$ winner       <fct> no, no, no, no, no, no, no, no, yes, no, no, no, no, no, …
$ inherit      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ num_char     <dbl> 1.231, 19.693, 0.596, 11.453, 7.813, 1.566, 15.420, 7.844…
$ line_breaks  <dbl> 29, 330, 33, 344, 97, 39, 595, 142, 134, 248, 279, 68, 38…
$ format       <dbl> 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, …
$ re_subj      <dbl> 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, …
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, …
$ urgent_subj  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 1, 4, 2, 4, 1, 3, 9, 6, 10, 0, 2, 16, 0, 1, 4, 4, 0, 8, 4…
$ number       <chr> "none", "big", "small", "big", "small", "small", "big", "…

Now that our testing and training data sets have been built, let’s practice picking a model!

1. Refit the first model with the training data. Next, fit the other additive generalized linear model below (you have fit email_fit above). Name these models email_fit and email_fit2

email_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ exclaim_mess + winner, data = train_data, family = "binomial")

email_fit2 <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ exclaim_mess + image , data = train_data, family = "binomial")

Prediction

Now, let’s evaluate our models using our test data using the following code below. Comment on what the code is doing…

email_pred <- predict(email_fit, test_data, type = "prob") |>  
  bind_cols(test_data |> select(spam))  

How can we plot this?

Make an Receiver operating characteristic (ROC) curve (plot true positive rate vs false positive rate)

email_pred |>
  roc_curve(
    truth = spam, 
    .pred_1, 
    event_level = "second" #which level is a success?
  ) |>
  autoplot()

What is this ROC curve telling us? How was the ROC curve created?

The relationship at different cutoffs between true positive and false positives

## all of the thresholds and predictions are in these data here

email_pred |>
  roc_curve(
    truth = spam, 
    .pred_1, 
    event_level = "second" #which level is a success?
  ) 

# A tibble: 47 × 3
      .threshold specificity sensitivity
           <dbl>       <dbl>       <dbl>
 1 -Inf              0             1    
 2    0.00000952     0             1    
 3    0.0000144      0.00280       1    
 4    0.0000217      0.00420       1    
 5    0.0000494      0.00420       0.984
 6    0.0000917      0.00560       0.984
 7    0.000138       0.00700       0.984
 8    0.000209       0.00840       0.984
 9    0.000257       0.0126        0.984
10    0.000315       0.0182        0.984
# … with 37 more rows

email_pred |>
  arrange(.pred_1)

# A tibble: 778 × 3
   .pred_0    .pred_1 spam 
     <dbl>      <dbl> <fct>
 1    1.00 0.00000952 0    
 2    1.00 0.00000952 0    
 3    1.00 0.0000144  0    
 4    1.00 0.0000217  1    
 5    1.00 0.0000494  0    
 6    1.00 0.0000917  0    
 7    1.00 0.000138   0    
 8    1.00 0.000209   0    
 9    1.00 0.000209   0    
10    1.00 0.000209   0    
# … with 768 more rows

Area under the curve

We can calculate the area under the curve using the following code:

email_pred |>
  roc_auc(
    truth = spam, 
    .pred_1, 
    event_level = "second" #which level is a success
  ) 

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.663

What is the AUC?

0.663

There are two things we can do with this number…

– Is this number > 0.5?

– How does this number compare to another AUC calculation?

Check Linear Regression Models

What if we don’t have a testing data set?

These are the data our model were trained on. Not optimal for assessing performance but it is something.

Even if we don’t have a test data set, we could still create a new column of predictions like before:

Context of Penguins data set

# predict based on new data

myPredictiveModel <- linear_reg() |>
  set_engine("lm") |>
  fit(body_mass_g ~ flipper_length_mm, data = penguins)

predict_peng <- penguins |>
  mutate(myPrediction = predict(myPredictiveModel, penguins)$.pred)

From here we can plot \(\hat{y}\) vs \(y\):

predict_peng |>
  ggplot(aes(x = body_mass_g, y = myPrediction)) +
  geom_point() +
  labs(x = "True Body Mass", y = "Predicted Body Mass", title = "Predicted vs True Body Mass") +
  geom_abline(slope = 1, intercept = 0, color = "steelblue")

Warning: Removed 2 rows containing missing values (`geom_point()`).

Assumptions of Linear Regression

Alternatively, we could create a residual plot. Residual plots can be used to assess whether a linear model is appropriate.

A common assumption of linear regression models is that the error term, \(\epsilon\), has constant variance everywhere.

• If the linear model is appropriate, a residual plot should show this.

• Patterned or non-constant residual spread may sometimes be indicative a model is missing predictors or missing interactions.

Residuals

Create a new column residuals in predict_peng and save your data frame as predict_peng_2

predict_peng_2 <- predict_peng |>
  mutate(residuals = body_mass_g - myPrediction)

The Plot

predict_peng_2 |>
  ggplot(aes(x = myPrediction, y = residuals)) + 
  geom_point() +
  geom_hline(yintercept = 0) +
  labs(x = "Predicted body_mass", y = "Residual")

Warning: Removed 2 rows containing missing values (`geom_point()`).

Note: If you encounter a residual plot where the points in the plot have a curved pattern, it likely means that the regression model you have specified for the data is not correct.