MLR - Logistic Regression
Day 10
Dr. Elijah Meyer
Duke University
STA 199 - Summer 2023
June 8th
Checklist
– Clone ae-10
– Homework 3 Due Tuesday (6-13)
– Project Proposal due Monday (6-12)
— Turn in on GitHub
— Lab today is a project work day
Warm Up: Question 1
– What is the main difference between Simple Linear Regression and Multiple Linear Regression?
Warm Up: Question 2
– What is the main difference between an additive model and an interaction model?
Goals
– Understand R-squared vs Adjusted R-squared
– What, why and how of logistic regression
More about R-Squared vs Adjusted R-Squared
R-squared has…
A meaningful definition
a relationship with
corwhen in the SLR case
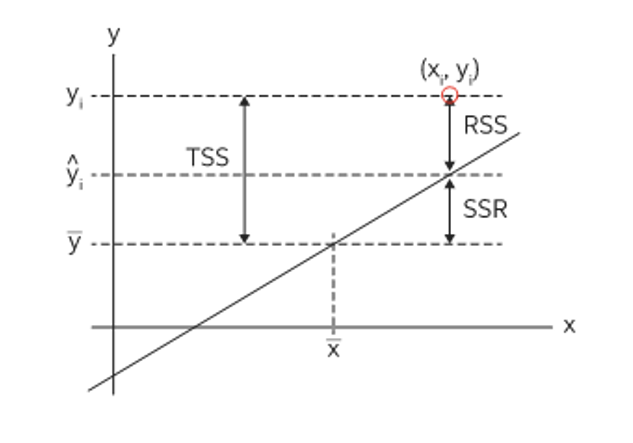
R-Squared
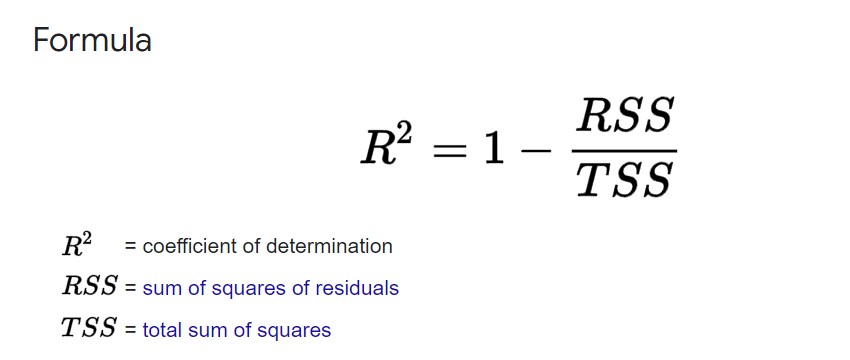
R-squared
More about R-Squared vs Adjusted R-Squared
When can we use R-squared for model selection?
When models have the same number of variables
Why can’t we use it to compare models with different number of variables? See ae-09 for demonstration.
R-squared: Takeaway
– statistical measure in a regression model that determines the proportion of variance in the response variable that can be explained by the explanatory variable(s).
– The more variables you include, the larger the R-squared value will be (always)
More about R-Squared vs Adjusted R-Squared
Adjusted R-squared …
Doesn’t have a clean definition
Is very useful for model selection
Adjusted R-Squared
Takeaway: Adds a penalty for “unimportant” predictors (x’s)

Any questions?
Finish MLR
– clone ae-10
– finish MLR (2 quantitative explanatory variables)
Logistic Regression
Goals
– The What, Why, and How of Logistic Regression
What is Logistic Regreesion
Similar to linear regression…. but
Modeling tool when our response is categorical
What we will do today
– This type of model is called a generalized linear model
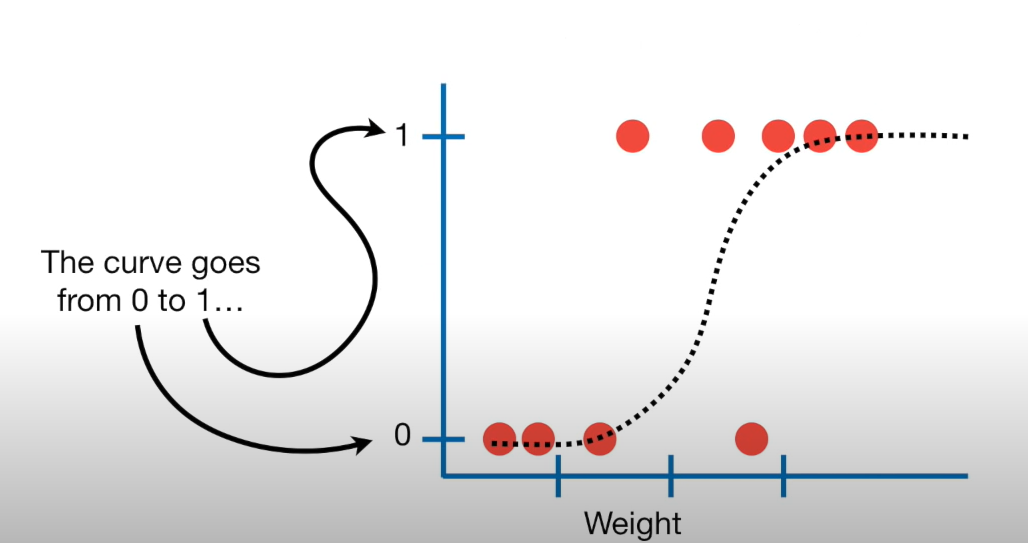
Start from the beginning
Terms
– Bernoulli Distribution
2 outcomes: Success (p) or Failure (1-p)
\(y_i\) ~ Bern(p)
What we can do is we can use our explanatory variable(s) to model p
2 Steps
– 1: Define a linear model
– 2: Define a link function
A linear model
\(\eta_i = \beta_o + \beta_1*X_i + ...\)
Note: \(\eta_i\) is some response of our linear model
But we can’t stop here… \(\eta_i\) isn’t the probability of success of our response
Think about what a linear model looks like
Next steps
– Preform a transformation to our response variable so it has the appropriate range of values
– “Link” our linear model to the paramater of the outcome distribution
– \(y_i\) ~ Bern(p)
Generalized linear model
- Next, we need a link function that relates the linear model to the parameter of the outcome distribution i.e. transform the linear model to have an appropriate range
Logit Link Function
The logit link function is defined as follows:

\(\eta_i\) = \(log (\frac{p}{1-p})\)
– Note: log is in reference to natural log
Logit Link function
– A logit link function transforms the probabilities of the levels of a categorical response variable to a continuous scale that is unbounded
– Note: log is in reference to natural log
What’s this look like
Takes a [0,1] probability and maps it to log odds (-\(\infty\) to \(\infty\).)
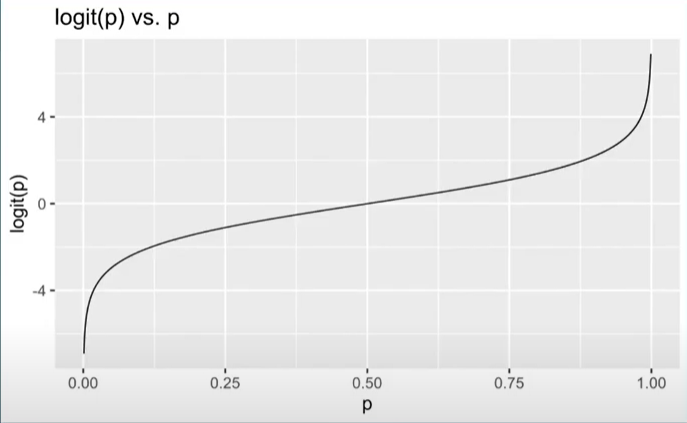
Almost….
This isn’t exactly what we need though…..
Will help us get to our goal
So we have a generalized linear model (GLM)
\(logit(p_i)\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1_i + ....\)
logit(p) is also known as the log-odds
logit(p) = \(log(\frac{p}{1-p})\)
\(log(\frac{p}{1-p})\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
One final fix
– Recall, the goal is to take values between -\(\infty\) and \(\infty\) and map them to probabilities. We need the opposite of the link function… or the inverse
– How do we take the inverse of a natural log?
- Taking the inverse of the logit function will map arbitrary real values back to the range [0, 1]
So
We need to take the inverse of the logit function
- \[log(\frac{p}{1-p}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\]
Math Time
Inverse Logit Link
Example Figure:
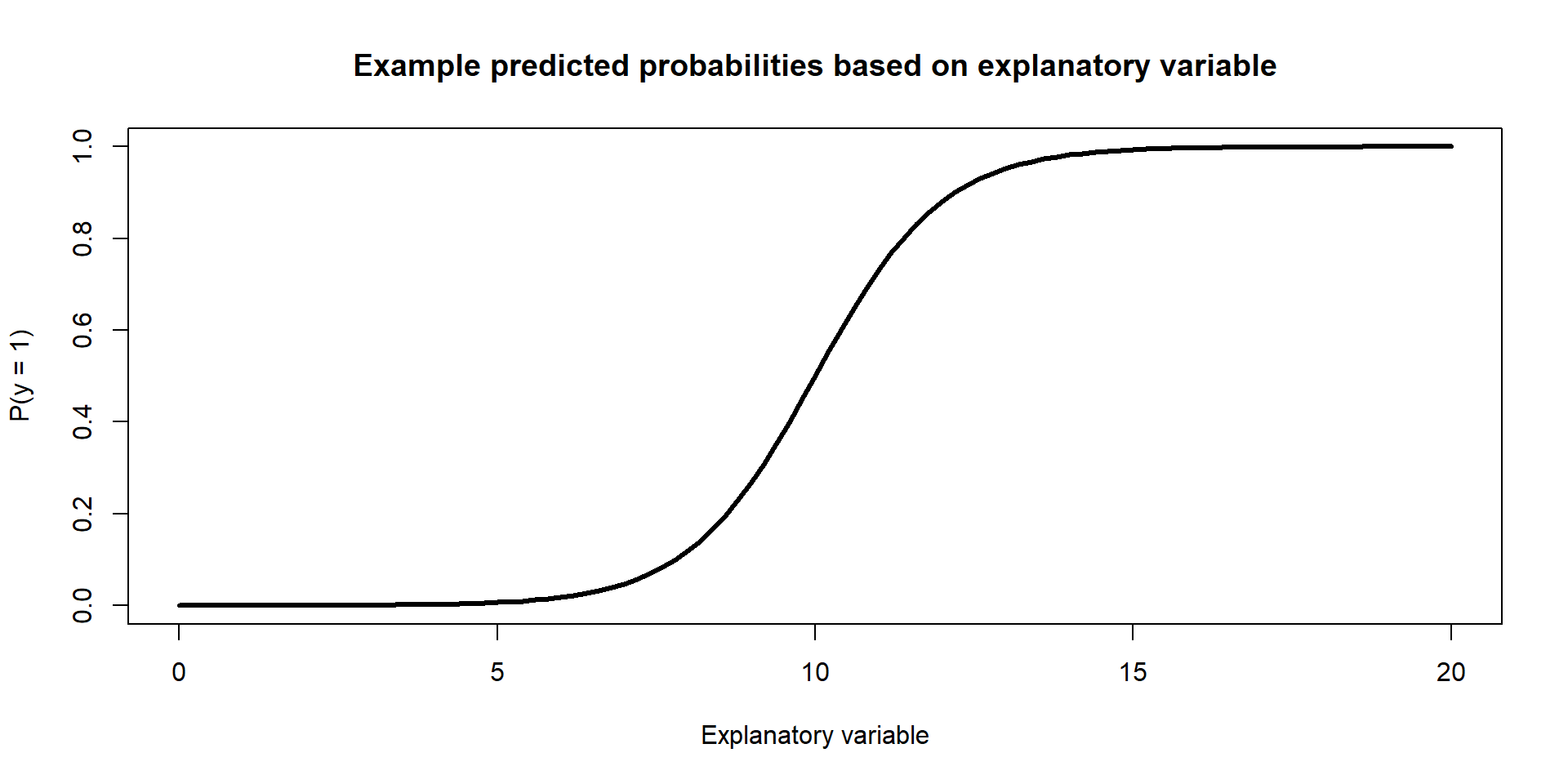
What we will do today
Calculate probabilities of success of a response based on values of explanatory variable x.

