Intro to Inference
Day 12
Dr. Elijah Meyer
Duke University
STA 199 - Summer 2023
June 13th
Checklist
– Clone ae-12
– Homework 3 Due tonight 11:59 (6-13)
– Project Proposal Feedback Soon
– Lab due Thursday 5:00 (6-15)
— Issues
– Group Feedback Survey in Sakai Coming Today (look for announcement)
– Exam 1 common mistakes to be posted on Slack today
– Exam 2: June 15th Start | June 20th due date
Warm Up
Last class, we fit a model to predict
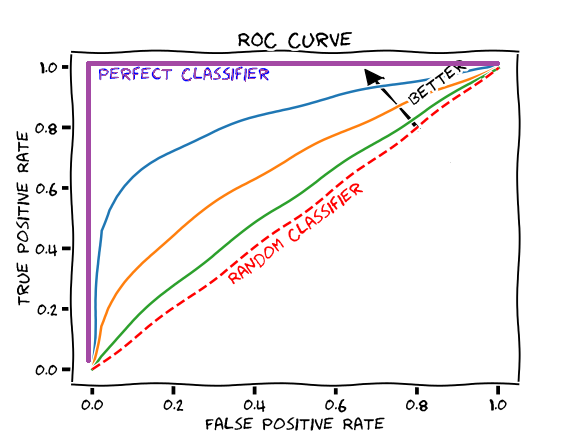
Warm Up
Go to ae-12. Go to the roc.qmd
Create your own roc curve using email_fit2.
Compare the predictive performance to email_fit.
Is this new model better? Worse? How can you tell?
Statistical Inference
– the methods of forming judgments about population parameters
Population Parameters
– \(\mu\)
– \(\pi\)
Population Parameters
– \(\mu_1 - \mu_2\)
– \(\pi_1 - \pi_2\)
Motivation
But…. we don’t know what these values are, so we collect data!
Sample Statistics
– \(\bar{x}\)
– \(\hat{p}\)
Sample Statistics
– \(\bar{x_1} - \bar{x_2}\)
– \(\hat{p_1} - \hat{p_2}\)
Questions that we will answer
– Test to see if our population parameter is different than a value (hypothesis testing)
– Estimate the value of the population parameter
and we will use data and the idea of variability to answer these questions
Today
We will go through how to conduct a hypothesis test using bootstrapping procedures!
Bootstrap & Randomization
Bootstrapping is a statistical procedure that re samples within a single data set to create many simulated samples.
The term bootstrapping comes from the phrase “pulling oneself up by one’s bootstraps”, which is a metaphor for accomplishing an impossible task without any outside help
Randomization is when we randomly shuffle within a single data set to create many simulated samples
Why
Impossible task: estimating / testing a population parameter using data from only the given sample.
Note: This notion of saying something about a population parameter using only information from an observed sample is the crux of statistical inference.
Hypothesis Testing
– Null hypothesis \(H_o:\)
– Alternative hypothesis \(H_a:\)
Null hypothesis
– Assumes “nothing is going on”
– Sets a parameter = 0
– Sets group equal to each other
Alternative hypothesis
– This is what we are interested in!
– We dictate this by the sign of our alternative hypothesis
Alternative hypothesis
– >
– <
– \(\neq\)
ae-12
– p-value
– significance level
– Decisions; Conclusions; Interpretations
When can we trust these results?
– When the sample we take is representative
We have a random sample
Sample size is not very small
ae-12
Can you read Martian? Bumba & Kiki
Alone, please think about which option is Bumba

